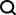Die Fibonacci-Reihe in C# in der Fibonacci-Reihe ist eine der bekanntesten Sequenzreihen. Die Reihenfolge ist 0, 1, 1, 2, 3, 5, 8…. Die Fibonacci-Reihe beginnt bei Null und Eins und die n?chste Zahl ist die Summe zweier vorhergehender Zahlen. Es hei?t, dass die Fibonacci-Reihe im 13. Jahrhundert von Leonardo Pisano Bigollo geschaffen wurde. Für einige Szenarien ist die Fibonacci-Reihe nützlich. Grunds?tzlich wurde es ursprünglich zur L?sung des Kaninchenproblems verwendet, d. h. der Anzahl der aus einem Paar geborenen Kaninchen. Es gibt auch andere Probleme, bei denen die Fibonacci-Folge nützlich ist. Logik der Fibonacci-Reihe
Wie in der Fibonacci-Reihe ist die Zahl die Summe ihrer beiden vorhergehenden Zahlen. Wenn wir also eine Fibonacci-Reihe haben, sagen wir 0, 1, 1, 2, 3, 5, 8, 13, 21 ... Demnach w?re die n?chste Zahl die Summe der beiden vorhergehenden Zahlen wie 13 und 21. Die n?chste Zahl ist also 13 +21=34.
Hier ist die Logik zum Generieren von Fibonacci-Reihen
F(n)= F(n-1) +F(n-2)
Wobei F(n) die Termnummer und F(n-1) +F(n-2) eine Summe vorhergehender Werte ist.
Wenn wir also die Serien 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 haben …
Gem?? der Logik F(n)= F(n-1) +F(n-2)
F(n)= 55+89
F(n)= 144
Der n?chste Begriff w?re 144.
Verschiedene Methoden zur Erstellung von Fibonacci-Reihen
Fibonacci-Reihen k?nnen auf verschiedene Arten generiert werden.
1. Iterativer Ansatz
Dieser Weg ist der einfachste Weg, Serien zu generieren.
Code:2. Rekursive Methode
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespaceFibonacciDemo
{
classProgram
{
staticint Fibonacci(int n)
{
intfirstnumber = 0, secondnumber = 1, result = 0;
if (n == 0) return 0; //It will return the first number of the series
if (n == 1) return 1; // it will return ?the second number of the series
for (int i = 2; i<= n; i++)? // main processing starts from here
{
result = firstnumber + secondnumber;
firstnumber = secondnumber;
secondnumber = result;
}
return result;
}
staticvoid Main(string[] args)
{
Console.Write("Length of the Fibonacci Series: ");
int length = Convert.ToInt32(Console.ReadLine());
for(int i = 0; i< length; i++)
{
Console.Write("{0} ", Fibonacci(i));
}
Console.ReadKey();
}
}
}
Dies ist eine weitere Methode zur L?sung dieses Problems.
Methode 1
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespaceFibonacciDemo
{
classProgram
{
staticint Fibonacci(int n)
{
intfirstnumber = 0, secondnumber = 1, result = 0;
if (n == 0) return 0; //it will return the first number of the series
if (n == 1) return 1; // it will return the second number of the series
return Fibonacci(n-1) + Fibonacci(n-2);
}
staticvoid Main(string[] args)
{
Console.Write("Length of the Fibonacci Series: ");
int length = Convert.ToInt32(Console.ReadLine());
for(int i = 0; i< length; i++)
{
Console.Write("{0} ", Fibonacci(i));
}
Console.ReadKey();
}
}
}Methode 2
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace FibonacciSeries
{
class Program
{
public static void Fibonacci
(
int firstnumber,
int secondnumber,
int count,
int length,
)
{
if (count <= length)
{
Console.Write("{0} ", firstnumber);
Fibonacci(secondnumber, firstnumber + secondnumber, count + 1, length);
}
}
public static void Main(string[] args)
{
Console.Write("Length of the Fibonacci Series: ");
int length = Convert.ToInt32(Console.ReadLine());
Fibonacci(0, 1, 1, length);
Console.ReadKey();
}
}
}Ausgabe:
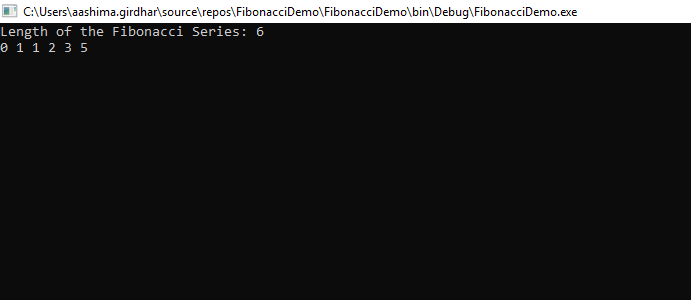 3. Fibonacci mithilfe von Array
3. Fibonacci mithilfe von Array
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
public class Program
{
public static int[] Fibonacci(int number)
{
int[] a = new int[number];
a[0] = 0;
a[1] = 1;
for (int i = 2; i < number; i++)
{
a[i] = a[i - 2] + a[i - 1];
}
return a;
}
public static void Main(string[] args)
{
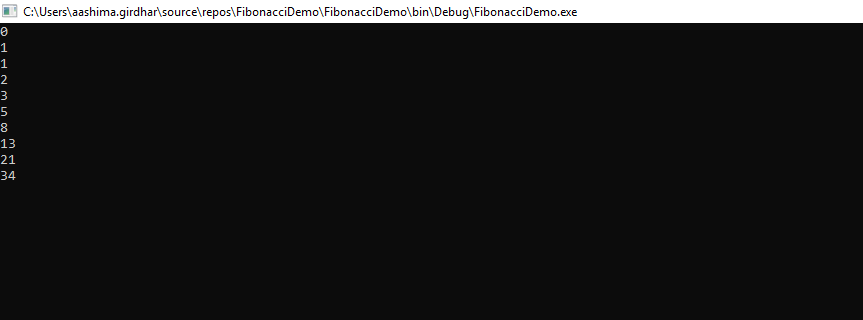
var b = Fibonacci(10);
foreach (var elements in b)
{
Console.WriteLine(elements);
}
}
}Ausgabe:
 Wie finde ich den N-ten Term der Fibonacci-Reihe?
Wie finde ich den N-ten Term der Fibonacci-Reihe?
Folgend sind die Methoden
Methode 1
Code:Der obige Code dient dazu, den n-ten Term in der Fibonacci-Reihe zu finden. Wenn wir beispielsweise den 12
using System;
namespace FibonacciSeries
{
class Program {
public static int NthTerm(int n)
{
if ((n == 0) || (n == 1))
{
return n;
}
else
{
return (NthTerm(n - 1) + NthTerm(n - 2));
}
}
public static void Main(string[] args)
{
Console.Write("Enter the nth term of the Fibonacci Series: ");
int number = Convert.ToInt32(Console.ReadLine());
number = number - 1;
Console.Write(NthTerm(number));
Console.ReadKey();
}
}
}tenTerm in der Reihe finden m?chten, w?re das Ergebnis 89. Methode 2
(O(Log t) Zeit).
Es gibt eine weitere Rekursionsformel, die verwendet werden kann, um die t-te Fibonacci-Zahl zu ermitteln. Wenn t gerade ist, dann = t/2:
F(t) = [2*F(k-1) + F(k)]*F(k)
Wenn t ungerade ist, dann ist k = (t + 1)/2
F(t) = F(k)*F(k) + F(k-1)*F(k-1)
Fibonacci-Matrix
Nachdem wir die Determinante erhalten haben, erhalten wir (-1)t = Ft+1Ft-1 – Ft2
FmFt + Fm-1Ft-1 = Fm+t-1
Indem man t = t+1 setzt,
FmFt+1 + Fm-1Ft = Fm+t
Setzen Sie m = t
F2t-1 = Ft2 + Ft-12
F2t = (Ft-1 + Ft+1)Ft = (2Ft-1 + Ft)Ft
Um die Formel zu erhalten, gehen wir wie folgt vor
Wenn t gerade ist, setzen Sie k = t/2
Wenn t ungerade ist, setzen Sie k = (t+1)/2
Durch das Sortieren dieser Zahlen k?nnen wir verhindern, dass der Speicherplatz von STACK st?ndig belegt wird. Es gibt die Zeitkomplexit?t von O(n) an. Der rekursive Algorithmus ist weniger effizient.
Code:Wenn nun der obige Algorithmus für n=4 ausgeführt wird
int f(n) : if( n==0 || n==1 ) return n; else return f(n-1) + f(n-2)
fn(4)
f(3)???????????? f(2)
f(2)?? f(1)???? f(1)?? f(0)
f(1)? f(0)
Es ist also ein Baum. Zur Berechnung von f(4) müssen wir f(3) und f(2) usw. berechnen. Für einen kleinen Wert von 4 wird f(2) zweimal und f(1) dreimal berechnet. Diese Anzahl der Erg?nzungen wird bei gro?en Zahlen zunehmen.
Es gibt eine Vermutung, dass die Anzahl der zur Berechnung von f (n) erforderlichen Additionen f (n+1) -1 betr?gt.
Fazit
Hier wird immer die Iterationsmethode bevorzugt, da sie einen schnelleren Ansatz zur L?sung dieser Art von Problemen bietet. Hier speichern wir die erste und die zweite Zahl der Fibonacci-Reihe in der vorherigen Zahl und der vorherigen Zahl (das sind zwei Variablen) und verwenden au?erdem die aktuelle Zahl, um die Fibonacci-Zahl zu speichern.
Das obige ist der detaillierte Inhalt vonFibonacci-Reihe in C#. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Hei?e KI -Werkzeuge

Undress AI Tool
Ausziehbilder kostenlos

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem v?llig kostenlosen KI-Gesichtstausch-Tool aus!

Hei?er Artikel

Hei?e Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Hei?e Themen
 Zufallszahlengenerator in C#
Sep 03, 2024 pm 03:34 PM
Zufallszahlengenerator in C#
Sep 03, 2024 pm 03:34 PM
Leitfaden zum Zufallszahlengenerator in C#. Hier besprechen wir die Funktionsweise des Zufallszahlengenerators, das Konzept von Pseudozufallszahlen und sicheren Zahlen.
 Der Unterschied zwischen Multithreading und asynchronem C#
Apr 03, 2025 pm 02:57 PM
Der Unterschied zwischen Multithreading und asynchronem C#
Apr 03, 2025 pm 02:57 PM
Der Unterschied zwischen Multithreading und Asynchron besteht darin, dass Multithreading gleichzeitig mehrere Threads ausführt, w?hrend asynchron Operationen ausführt, ohne den aktuellen Thread zu blockieren. Multithreading wird für rechenintensive Aufgaben verwendet, w?hrend asynchron für die Benutzerinteraktion verwendet wird. Der Vorteil des Multi-Threading besteht darin, die Rechenleistung zu verbessern, w?hrend der Vorteil von Asynchron nicht darin besteht, UI-Threads zu blockieren. Die Auswahl von Multithreading oder Asynchron ist von der Art der Aufgabe abh?ngt: Berechnungsintensive Aufgaben verwenden Multithreading, Aufgaben, die mit externen Ressourcen interagieren und die UI-Reaktionsf?higkeit asynchron verwenden müssen.
 C# gegen C: Geschichte, Evolution und Zukunftsaussichten
Apr 19, 2025 am 12:07 AM
C# gegen C: Geschichte, Evolution und Zukunftsaussichten
Apr 19, 2025 am 12:07 AM
Die Geschichte und Entwicklung von C# und C sind einzigartig, und auch die Zukunftsaussichten sind unterschiedlich. 1.C wurde 1983 von Bjarnestrustrup erfunden, um eine objektorientierte Programmierung in die C-Sprache einzuführen. Sein Evolutionsprozess umfasst mehrere Standardisierungen, z. B. C 11 Einführung von Auto-Keywords und Lambda-Ausdrücken, C 20 Einführung von Konzepten und Coroutinen und sich in Zukunft auf Leistung und Programme auf Systemebene konzentrieren. 2.C# wurde von Microsoft im Jahr 2000 ver?ffentlicht. Durch die Kombination der Vorteile von C und Java konzentriert sich seine Entwicklung auf Einfachheit und Produktivit?t. Zum Beispiel führte C#2.0 Generics und C#5.0 ein, die eine asynchrone Programmierung eingeführt haben, die sich in Zukunft auf die Produktivit?t und das Cloud -Computing der Entwickler konzentrieren.
 Primzahlen in C#
Sep 03, 2024 pm 03:35 PM
Primzahlen in C#
Sep 03, 2024 pm 03:35 PM
Leitfaden zu Primzahlen in C#. Hier besprechen wir die Einführung und Beispiele von Primzahlen in C# sowie die Codeimplementierung.
 So ?ndern Sie das Format von XML
Apr 03, 2025 am 08:42 AM
So ?ndern Sie das Format von XML
Apr 03, 2025 am 08:42 AM
Es gibt verschiedene M?glichkeiten, XML -Formate zu ?ndern: manuell mit einem Texteditor wie Notepad bearbeiten; automatisch Formatierung mit Online- oder Desktop -XML -Formatierungswerkzeugen wie XMLBeautifier; Definieren Sie Conversion -Regeln mithilfe von XML -Conversion -Tools wie XSLT; oder analysieren und mit Verwendung von Programmiersprachen wie Python arbeiten. Seien Sie vorsichtig, wenn Sie die Originaldateien ?ndern und sichern.
 Wie man XML in JSON umwandelt
Apr 03, 2025 am 09:09 AM
Wie man XML in JSON umwandelt
Apr 03, 2025 am 09:09 AM
Zu den Methoden zum Umwandeln von XML in JSON geh?ren: Schreiben von Skripten oder Programmen in Programmiersprachen (wie Python, Java, C#) zum Konvertieren; Einfügen oder Hochladen von XML -Daten mithilfe von Online -Tools (z. B. XML in JSON, Gojko XML Converter, XML Online -Tools) und Auswahl der JSON -Formatausgabe; Durchführung von Konvertierungsaufgaben mit XML mit JSON -Konvertern (wie Oxygen XML -Editor, Stylus Studio, Altova XMLSPY); Konvertieren von XML in JSON mithilfe von XSLT -Stylesheets; Verwenden von Datenintegrationstools (z. B. informatisch
 Was ist C# Multithreading -Programmierung? C# Multithreading -Programmierung verwendet C# Multithreading -Programmierung
Apr 03, 2025 pm 02:45 PM
Was ist C# Multithreading -Programmierung? C# Multithreading -Programmierung verwendet C# Multithreading -Programmierung
Apr 03, 2025 pm 02:45 PM
C# Multi-Thread-Programmierung ist eine Technologie, mit der Programme gleichzeitig mehrere Aufgaben ausführen k?nnen. Es kann die Programmeffizienz verbessern, indem es die Leistung verbessert, die Reaktionsf?higkeit verbessert und die parallele Verarbeitung implementiert. W?hrend die Thread -Klasse eine M?glichkeit bietet, Threads direkt zu erstellen, k?nnen erweiterte Tools wie Task und Async/Warted sicherer asynchroner Operationen und eine sauberere Codestruktur liefern. H?ufige Herausforderungen bei der Multithread -Programmierung umfassen Deadlocks, Rassenbedingungen und Ressourcenleckage, die eine sorgf?ltige Gestaltung von Fadenmodellen und die Verwendung geeigneter Synchronisationsmechanismen erfordern, um diese Probleme zu vermeiden.
 Wie man XML in Wort umwandelt
Apr 03, 2025 am 08:15 AM
Wie man XML in Wort umwandelt
Apr 03, 2025 am 08:15 AM
Es gibt drei M?glichkeiten, XML in Wort zu konvertieren: Verwenden Sie Microsoft Word, verwenden Sie einen XML -Konverter oder verwenden Sie eine Programmiersprache.